The Mathematics of Voting Systems
Mathematical perspectives on theories and practices of social choice
Prasad Senesi
Associate Professor, Department of Mathematics
The Catholic University of America
Sponsored by PSW Science Member Adarsh Deepak
About the Lecture
The mathematical foundations of the theory of social choice, or voting theory, were established in the late eighteenth century. Since then, this problem of aggregating choice has been studied from a wide variety of mathematical perspectives, using ideas from algebra, geometry, topology, and other fields. This lecture will provide a survey of some of these perspectives, beginning with a mathematical analysis of the distribution of power in the electoral college. The analysis provides some counterintuitive results in comparing the power of small and large states in Presidential elections. The lecture will also discuss alternatives to the standard ‘simple majority’ method of determining an election winner, and review some research into these methods with surprising mathematical depth and sophistication. After this foray into some of the deeper theoretical folds of social choice, the lecture will examine proposals for ranked choice voting currently being discussed here in America.
Suggested References:
(1) J. Banzhaf, “Weighted Voting Doesn’t Work: A Mathematical Analysis,” Rutgers Law Review, Vol. 19, No.2, 1965, pp. 317-343.
(2) J. Hodge and R. Klima, The Mathematics of Voting and Elections: A Hands-On Approach. American Mathematical Society, Providence, R.I., 2005.
(3) D. Saari, Decisions and Elections: Explaining the Unexpected. Cambridge University Press, Cambridge, MA, 2001.
About the Speaker

Prasad Senesi is an associate professor of mathematics at The Catholic University of America. Before joining the faculty at Catholic, he did postdoctoral work at the University of Ottawa.
Prasad’s research specialties include representation theory of Lie algebras, knot theory, voting theory, and mathematical modeling. His work in voting theory focuses on the mathematical foundations of positional voting systems, their geometric descriptions, and their connections with other structures in mathematics.
Prasad is an author on numerous publications in highly ranked mathematics journals, and he has given talks on his work to a wide range of audiences nationwide. Prasad earned his PhD in Mathematics at UC-Riverside.
Minutes
On October 23, 2020, by Zoom videoconference broadcast on the PSW Science YouTube channel, President Larry Millstein called the 2,427th meeting of the Society to order at 8:02 p.m. EDT. He announced the order of business and welcomed new members. The Recording Secretary then read the minutes of the previous meeting.
President Millstein then introduced the speaker for the evening, Prasad Senesi, Associate Professor of Mathematics at The Catholic University of America. His lecture was titled, “The Mathematics of Voting Systems: Mathematical perspectives on theories and practices of social choice.”
Senesi began with an overview of the Electoral College, whose electors elect the President of the United States. The College is a weighted voting system, apportioning to each state one elector for each of the state’s representatives in Congress. Although the District of Columbia has no voting representation in Congress, it is apportioned three electors in the Electoral College.
The states and D.C. are permitted to apportion their electors how they choose. Every jurisdiction except Nebraska and Maine apportion all of their electors to whichever presidential candidate wins the most votes in a given presidential election.
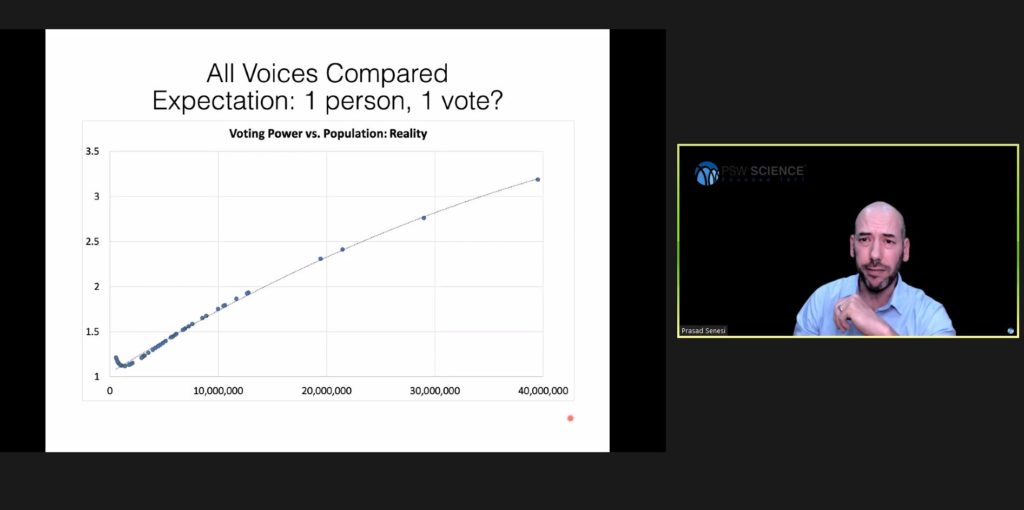
Because the population of each jurisdiction varies, Senesi sought to measure individual voter influence in the Electoral College voting system and, thus, individual voter influence in U.S. presidential elections.
Senesi then used the Treaty of Rome, which established the European Economic Community, to illustrate the dynamics of weighted voting theory. Senesi described the various country-coalitions that could carry any given measure in the treaty process. The Banzhaf number identifies the frequency with which a voter is critical in a given system. A voter is critical in a winning coalition if their defection costs the winning coalition its winning votes. Senesi identified the Banhzhaf power of the six Treaty of Rome countries each assigned between 1 and 4 votes. He then walked through the math to demonstrate that Banzhaf power is an expression of the probability that a voter has the deciding vote on an issue.
The Electoral College is a more complex weighted voting system. The system’s complexity makes it difficult to calculate the number of outcomes in which a state is critical divided by the total number of possible outcomes. Senesi therefore approximated probabilities using the Monte Carlo simulation to determine California, the state with the largest number of electors, had a 23.75% chance of being the deciding state in a presidential election.
Senesi then addressed the power of individual voters in a U.S. presidential election. To determine a voter’s probability of swinging an election, Senesi first calculated the probability the voter is critical in their state, and then the probability the voter’s state is critical in the Electoral College.
Applying Stirling’s formula approximates these numbers and indicates that a California voter is approximately three times more likely to cast the critical vote in a presidential election than a South Dakota voter. Senesi commented that at the level of the individual voter, more populous states are more influential in the Electoral College than less populous states. He then summarized various arguments both in favor and against changing the system for electing U.S. presidents.
While single-vote ballots are predominant in the U.S., there are more nuanced voting systems that allow voters to express the order of their preference for multiple candidates. Under the plurality method, the candidate with a plurality of first place votes wins. The method developed by Jean-Charles de Borda awards points to candidates depending on whether they are ranked first, second, or third on individual ballots, to elect the winner of the most points. Positional Voting expands the Borda methodology to assign points to every candidate on a ballot. Instant Runoff Voting or Ranked Choice Voting allows voters to rank their choice of candidates and eliminates candidates receiving the least number of votes until one candidate receives a majority of the votes. The Coombs method is similar to Ranked Choice Voting, but eliminates candidates in order of the greatest number of last-place votes they receive.
Senesi then evaluated each of the five voting systems he described using various theorems to identify potentially unsatisfactory results and means of manipulation. Despite their respective faults, each of the five methods is used in government and non-government elections around the world.
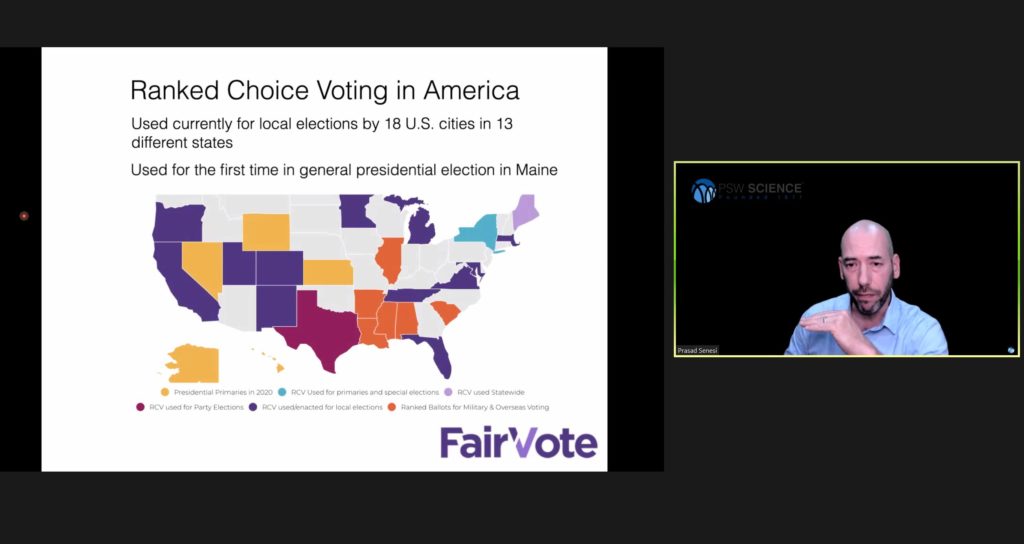
In the U.S., Ranked Choice Voting (or, RCV) has been the most popular alternative to single-vote ballots. In 1915, Ashtabula, Ohio became the first U.S. jurisdiction to use RCV, using it to elect their city council. In the decades that followed, of the 24 U.S. cities that adopted RCV, 23 repealed it. In recent years, however, RCV has rebounded in popularity.
RCV proponents argue that it limits the “spoiler” effect and incentivizes candidates to reach out to a broad spectrum of voters and reduce political polarization. This year, Maine will be the first state to use RCV in a general presidential election.
President Millstein then moderated questions from the online viewing audience. One member asked how various assumptions impacted the speaker’s individual voter power calculations. Senesi said more in-depth analysis of the numbers of eligible voters and voter turnout would impact his results. Another member asked the speaker about his recommendations for Electoral College reform. Sensei said existing inequities could be ameliorated by improving Electoral College apportionment. He noted the U.S. is now on its fifth different apportionment method to assign Congressional seats and, accordingly, Electoral College votes.
After the question and answer period, President Millstein thanked the speaker, made the usual housekeeping announcements, and invited guests to join the Society. At 9:43 p.m., President Millstein adjourned the meeting.
Temperature in Washington, D.C.: 20° C
Weather: Clear
Concurrent Viewers of the Zoom and YouTube live stream, 90 and views on the PSW Science YouTube and Vimeo channels: 186.
Respectfully submitted,
James Heelan, Recording Secretary
Highlights